
1
An Introduction to Isotopic Calculations
John M. Hayes (jhayes@whoi.edu)
Woods Hole Oceanographic Institution, Woods Hole, MA 02543, USA, 30 September 2004
Abstract. These notes provide an introduction to:
• Methods for the expression of isotopic abundances,
• Isotopic mass balances, and
• Isotope effects and their consequences in open and
closed systems.
Notation. Absolute abundances of isotopes are com-
monly reported in terms of atom percent. For example,
atom percent
13
C = [
13
C/(
12
C +
13
C)]100 (1)
A closely related term is the fractional abundance
fractional abundance of
13
C ≡
13
F
13
F
=
13
C/(
12
C +
13
C) (2)
These variables deserve attention because they provide
the only basis for perfectly accurate mass balances.
Isotope ratios are also measures of the absolute abun-
dance of isotopes; they are usually arranged so that the
more abundant isotope appears in the denominator
“carbon isotope ratio” =
13
C/
12
C ≡
13
R (3)
For elements with only two stable nuclides (H, C, and N,
for example), the relationship between fractional abun-
dances and isotope ratios is straightforward
13
R =
13
F/(1 -
13
F) (4)
13
F =
13
R/(1 +
13
R) (5)
Equations 4 and 5 also introduce a style of notation.
In mathematical expressions dealing with isotopes, it is
convenient to follow the chemical convention and to use
left superscripts to designate the isotope of interest, thus
avoiding confusion with exponents and retaining the
option of defining subscripts. Here, for example, we
have written
13
F rather than F
13
or F
13
.
Parallel version of equations 4 and 5 pertain to multi-
isotopic elements. In the case of oxygen, for example,
F
F
F
R
1817
18
18
1 −−
=
(4a)
RR
R
F
1817
18
18
1 ++
=
(5a)
Natural variations of isotopic abundances. The
isotopes of any element participate in the same chemical
reactions. Rates of reaction and transport, however,
depend on nuclidic mass, and isotopic substitutions
subtly affect the partitioning of energy within molecules.
These deviations from perfect chemical equivalence are
termed isotope effects. As a result of such effects, the
natural abundances of the stable isotopes of practically
all elements involved in low-temperature geochemical
(< 200°C) and biological processes are not precisely con-
stant. Taking carbon as an example, the range of interest
is roughly 0.00998 ≤
13
F ≤ 0.01121. Within that range,
differences as small as 0.00001 can provide information
about the source of the carbon and about processes in
which the carbon has participated.
The delta notation. Because the interesting isotopic
differences between natural samples usually occur at and
beyond the third significant figure of the isotope ratio, it
has become conventional to express isotopic abundances
using a differential notation. To provide a concrete
example, it is far easier to say – and to remember – that
the isotope ratios of samples A and B differ by one part
per thousand than to say that sample A has 0.3663 %
15
N
and sample B has 0.3659 %
15
N. The notation that pro-
vides this advantage is indicated in general form below
[this means of describing isotopic abundances was first
used by Urey (1948) in an address to the American
Association for the Advancement of Science, and first
formally defined by McKinney et al. (1950)]
δ
A
X
STD
= 1
STD
A
Sample
A
−
R
R
(6)
Where
δ
expresses the abundance of isotope A of ele-
ment X in a sample relative to the abundance of that
same isotope in an arbitrarily designated reference mater-
ial, or isotopic standard. For hydrogen and oxygen, that
reference material was initially Standard Mean Ocean
Water (
SMOW). For carbon, it was initially a particular
calcareous fossil, the PeeDee Belemnite (
PDB; the same
standard served for oxygen isotopes in carbonate miner-
als). For nitrogen it is air (
AIR). Supplies of PDB and of
the water that defined
SMOW have been exhausted. Prac-
tical scales of isotopic abundance are now defined in
terms of surrogate standards distributed by the Interna-
tional Atomic Energy Authority’s laboratories in Vienna.
Accordingly, modern reports often present values of
δ
VSMOW
and
δ
VPDB
. These are equal to values of
δ
SMOW
and
δ
PDB
.
The original definition of
δ
(McKinney et al., 1950)
multiplied the right-hand side of equation 6 by 1000.
Isotopic variations were thus expressed in parts per thou-
sand and assigned the symbol ‰ (permil, from the Latin
per mille by analogy with per centum, percent). Equa-
2
tions based on that definition are often littered with
factors of 1000 and 0.001. To avoid this, it is more con-
venient to define δ as in equation 6. According to this
view (represented, for example, by Farquhar et al., 1989
and Mook, 2000), the ‰ symbol implies the factor of
1000 and we can equivalently write either
δ
= -25‰ or
δ
= -0.025.
To avoid clutter in mathematical expressions, sym-
bols for
δ
should always be simplified. For example,
δ
b
can represent
δ
13
C
PDB
(
-
3
HCO ). If multiple elements and
isotopes are being discussed, variables like
13
δ
and
15
δ
are explicit and allow use of right subscripts for desig-
nating chemical species.
Mass-Balance Calculations. Examples include (i)
the calculation of isotopic abundances in pools derived
by the combination of isotopically differing materials,
(ii) isotope-dilution analyses, and (iii) the correction of
experimental results for the effects of blanks. A single,
master equation is relevant in all of these cases. Its
concept is rudimentary: Heavy isotopes in product =
Sum of heavy isotopes in precursors. In mathematical
terms:
m
Σ
F
Σ
= m
1
F
1
+ m
2
F
2
+ ... (7)
where the m terms represent molar quantities of the ele-
ment of interest and the F terms represent fractional iso-
topic abundances. The subscript Σ refers to total sample
derived by combination of subsamples 1, 2, ... etc. The
same equation can be written in approximate form by
replacing the Fs with δs. Then, for any combination of
isotopically distinct materials:
δ
Σ
= Σm
i
δ
i
/Σm
i
(8)
Equation 8, though not exact, will serve in almost all
calculations dealing with natural isotopic abundances.
The errors can be determined by comparing the results
obtained using equations 7 and 8. Taking a two-
component mixture as the simplest test case, errors are
found to be largest when
δ
Σ
differs maximally from both
δ
1
and
δ
2
, i. e., when m
1
= m
2
. For this worst case, the
error is given by
δ
Σ
-
δ
Σ*
= (R
STD
)[(
δ
1
-
δ
2
)/2]
2
(9)
Where
δ
Σ
is the result obtained from eq. 8;
δ
Σ*
is the
exact result, obtained by converting
δ
1
and
δ
2
to frac-
tional abundances, applying eq. 7, and converting the
result to a
δ
value; and R
STD
is the isotopic ratio in the
standard that establishes the zero point for the
δ
scale
used in the calculation. The errors are always positive.
They are only weakly dependent on the absolute value of
δ
1
or
δ
2
and become smaller than the result of eq. 9 as
δ
>> 0. If R
STD
is low, as for
2
H (
2
R
VSMOW
= 1.5 × 10
-4
),
the errors are less than 0.04‰ for any |
δ
1
-
δ
2
| ≤ 1000‰.
For carbon (
13
R
PDB
= 0.011), errors are less than 0.03‰
for any |
δ
1
-
δ
2
| ≤ 100‰.
The excellent accuracy of eq. 8 does not mean that all
simple calculations based on
δ
will be similarly accurate.
As noted in a following section, particular care is
required in the calculation and expression of isotopic
fractionations. And, when isotopically labeled materials
are present, calculations based on
δ
should be avoided in
favor of eq. 7.
Isotope dilution. In isotope-dilution analyses, an
isotopic spike is added to a sample and the mixture is
then analyzed. The original “sample” might be a
material from which a representative subsample could be
obtained but which could not be quantitatively isolated
(say, total body water). For the mixture (Σ) of the
sample (x) and the spike (k), we can write:
(m
x
+ m
k
)F
Σ
= m
x
F
x
+ m
k
F
k
(10)
Rearrangement yields an expression for m
x
(e. g., moles
of total body water) in terms of m
k
, the size of the spike,
and measurable isotopic abundances:
m
x
= m
k
(F
k
- F
Σ
)/(F
Σ
- F
x
) (11)
Since we are dealing here with a mass balance,
δ
can be
substituted for F unless heavily labeled spikes are
involved.
Blank corrections. When a sample has been con-
taminated during its preparation by contributions from an
analytical blank, the isotopic abundance actually deter-
mined during the mass spectrometric measurement is that
of the sample plus the blank. Using Σ to represent the
sample prepared for mass spectroscopic analysis and x
and b to represent the sample and blank, we can write
m
Σ
δ
Σ
= m
x
δ
x
+ m
b
δ
b
(12)
Substituting m
x
= m
Σ
- m
b
and rearranging yields
δ
Σ
=
δ
x
- m
b
(
δ
x
-
δ
b
)/n
Σ
(13)
an equation of the form y = a + bx. If multiple analyses
are obtained, plotting
δ
Σ
vs. 1/m
Σ
will yield the accurate
(i. e., blank-corrected) value of
δ
x
as the intercept.
Calculations related to isotope effects
An isotope effect is a physical phenomenon. It
cannot be measured directly, but its consequences – a
partial separation of the isotopes, a fractionation – can
sometimes be observed. This relationship is indicated
schematically in Figure 1.
Fractionation. Two conditions must be met before
an isotope effect can result in fractionation. First, the
system in which the isotope effect is occurring must be
arranged so that an isotopic separation can occur. If a
reactant is transformed completely to yield some pro-
duct, an isotopic separation which might have been

3
visible at some intermediate point will not be observable
because the isotopic composition of the product must
eventually duplicate that of the reactant. Second, since
isotope effects are small enough that they don’t upset
blanket statements about chemical properties, the tech-
niques of measurement must be precise enough to detect
very small isotopic differences.
Observed fractionations are proportional to the mag-
nitudes of the associated isotope effects. Examples of
equilibrium and kinetic isotope effects are shown in
Figure 2. As indicated, the magnitude of an equilibrium
isotope effect can be represented by an equilibrium con-
stant. In this example, the reactants and products are
chemically identical (carbon dioxide and bicarbonate in
each case). However, due to the isotope effect, the equi-
librium constant is not exactly 1. There is, however, a
problem with the use of equilibrium constants to quantify
isotope effects. An equilibrium constant always pertains
to a specific chemical reaction, and, for any particular
isotopic exchange, the reaction can be formulated in
various ways, for example:
H
2
18
O + 1/3 CaC
16
O
3
' H
2
16
O + 1/3 CaC
18
O
3
(14)
vs.
H
2
18
O + CaC
16
O
3
' H
2
16
O + CaC
18
O
16
O
2
(15)
To avoid such ambiguities, EIEs are more commonly
described in terms of fractionation factors.
A fractionation factor is always a ratio of isotope
ratios. For the example in Figure 2, the fractionation
factor would be:
23
23
CO
12
13
HCO
12
13
CO/HCO
C
C
C
C
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
−
−
α
(16)
A more compact and typical representation would be
13
α
b/g
= R
b
/R
g
(17)
Here, subscripts have been used to designate the
chemical species (b for bicarbonate, g for gas-phase
CO
2
) and the superscript 13 indicates that the exchange
of
13
C is being considered. The resulting equation is
more compact. It does not combine chemical and math-
ematical systems of notation and, as a result, is less
cluttered and more readable. For either reaction 14 or
15, the fractionation factor would be
18
α
c/w
= R
c
/R
w
(18)
where c and w designate calcite and water, respectively.
For a kinetic isotope effect, the fractionation factor is
equal to the ratio of the isotope-specific rate constants. It
is sometimes denoted by
β
rather than
α
. In physical
organic chemistry and enzymology, however,
β
is gener-
ally reserved for the ratio of isotope-specific equilibrium
constants while
α
stands as the observed isotopic frac-
tionation factor.
There are no firm conventions about what goes in the
numerator and the denominator of a fractionation factor.
For equilibrium isotope effects it’s best to add subscripts
to
α
in order to indicate clearly which substance is in the
numerator and, for kinetic isotope effects, readers must
examine the equations to determine whether an author
has placed the heavy or the light isotope in the
numerator.
Reversibility and systems. Given a fractionation
factor, isotopic compositions of reactants and products
can usually be calculated once two questions have been
answered:
1. Is the reaction reversible?
2. Is the system open or closed?
Figure 2. Examples of equilibrium and kinetic
isotope effects.
Figure 1. Schematic representation of the relation-
ship between an isotope effect (a physical phenom-
enon) and the occurrence of isotopic fractionation (an
observable quantity).

4
An open system is one in which both matter and energy
are exchanged with the surroundings. In contrast, only
energy crosses the boundaries of a closed system.
Reversibility and openness vs. closure are key con-
cepts. Each is formally crisp, but authors often sew
confusion. If a system is described as “partially closed,”
readers should be on guard. If the description means that
only some elements can cross the boundaries of the
system, the concept might be helpful. If partial closure
instead refers to impeded transport of materials into and
out of the system, the concept is invalid and likely to
cause problems.
Openness covers a range of possibilities. Some open
systems are at steady state, with inputs and outputs
balanced so that the inventory of material remains
constant. In others, there are no inputs but products are
lost as soon as they are created. These cases can be
treated simply, others require specific models.
Reversible reaction, closed system. In such a
system, (1) the isotopic difference between products and
reactants will be controlled by the fractionation factor
and (2) mass balance will prevail.
To develop a quantitative treatment, we will consider
an equilibrium between substances A and B,
A
' B (19)
The isotopic relationship between these materials is
defined in terms of a fractionation factor:
1
1
B
A
B
A
A/B
+
+
==
δ
δ
α
R
R
(20)
where the Rs are isotope ratios and the
δ
s are the
corresponding
δ
values on any scale of abundances (the
same scale must be used for both the product and the
reactant). The requirement that the inventory of mater-
ials remain constant can be expressed inexactly, but with
good accuracy, in terms of a mass-balance equation:
δ
Σ
= f
B
δ
B
+ (1 – f
B
)
δ
A
(21)
where
δ
Σ
refers to the weighted-average isotopic com-
position of all of the material involved in the equilibrium
(for equation 14 or 15, it would refer to all of the oxygen
in the system) and f
B
refers to the fraction of that
material which is in the form of B. By difference, the
fraction of material in the form of A is 1 – f
B
.
Rearrangement of equation 20 yields:
δ
A
=
α
A/B
δ
B
+ (
α
A/B
– 1) (22)
The second term on the right-hand side of this equation
is commonly denoted by a special symbol:
α
- 1 ≡
ε
(23)
Equation 22 then becomes:
δ
A
=
α
A/B
δ
B
+
ε
A/B
(24)
(Like
δ
,
ε
is often expressed in parts per thousand. For
example, if
α
= 1.0077, then
ε
= 0.0077 or 7.7‰.
Dimensional analysis reliably indicates the form required
in any calculation. In equations 24-29, all terms could be
dimensionless or could be expressed in permil units.
The dimensionless form is required in equation 20,
where
δ
is added to a dimensionless constant, in equa-
tions 39 and 40, where use of permil units would unbal-
ance the equations, and in equations 41 and 42, where
δ
and/or
ε
appear as exponents or in the arguments of
transcendental functions.)
Substituting for δ
A
in equation 21, we obtain
δ
Σ
= f
B
δ
B
+ (1 – f
B
)(
α
A/B
δ
B
+
ε
A/B
) (25)
Solving for δ
B
, we obtain an expression which allows
calculation of δ
B
as a function of f
B
, given
α
A/B
and
δ
Σ
:
BBA/B
A/BB
B
1
1
f)f(
)f(
+−
−
−
=
Σ
α
ε
δ
δ
(26)
If equation 24 is rearranged to express
δ
B
in terms of
δ
A
,
α
A/B
, and
ε
A/B
, and the result is substituted for
δ
B
in
equation 21, we obtain a complementary expression for
δ
A
:
BBA/B
A/BBA/B
A
)1( ff
f
+−
+
=
Σ
α
εδα
δ
(27)
Equations 26 and 27 are generally applicable but
rarely employed because adoption of the approximation
α
A/B
≈ 1 yields far simpler results, namely:
δ
A
=
δ
Σ
+ f
B
ε
A/B
(28)
and
δ
B
=
δ
Σ
- (1 – f
B
)
ε
A/B
(29)
Graphs depicting these relationships can be constructed
very easily. An example is shown in Figure 3. For f
B
=
1 we must have
δ
B
=
δ
Σ
and for f
B
= 0 we must have
δ
A
=
δ
Σ
. As shown in Figure 3, the intercepts for the other
ends of the lines representing
δ
A
and
δ
B
will be
δ
Σ
±
ε
A/B
. If
α
A/B
< 1,
ε
A/B
will be negative and A will be
isotopically depleted relative to B. The lines represent-
ing
δ
A
and
δ
B
will slope upward as f
B
→ 0. If
α
A/B
> 1
then A would be enriched relative to B and the lines
would slope downward.
There are two circumstances in which the approxi-
mation leading to equations 28 and 29 (i. e.,
α
A/B
≈ 1)
must be examined. The first involves highly precise stu-
dies and the second almost any hydrogen-isotopic frac-
tionations. As an example of the first case, Figure 4
compares the results of equations 26 and 27 to those of
28 and 29 for a system with
α
A/B
= 1.0412. This is, in
fact, the fractionation factor for the exchange of oxygen
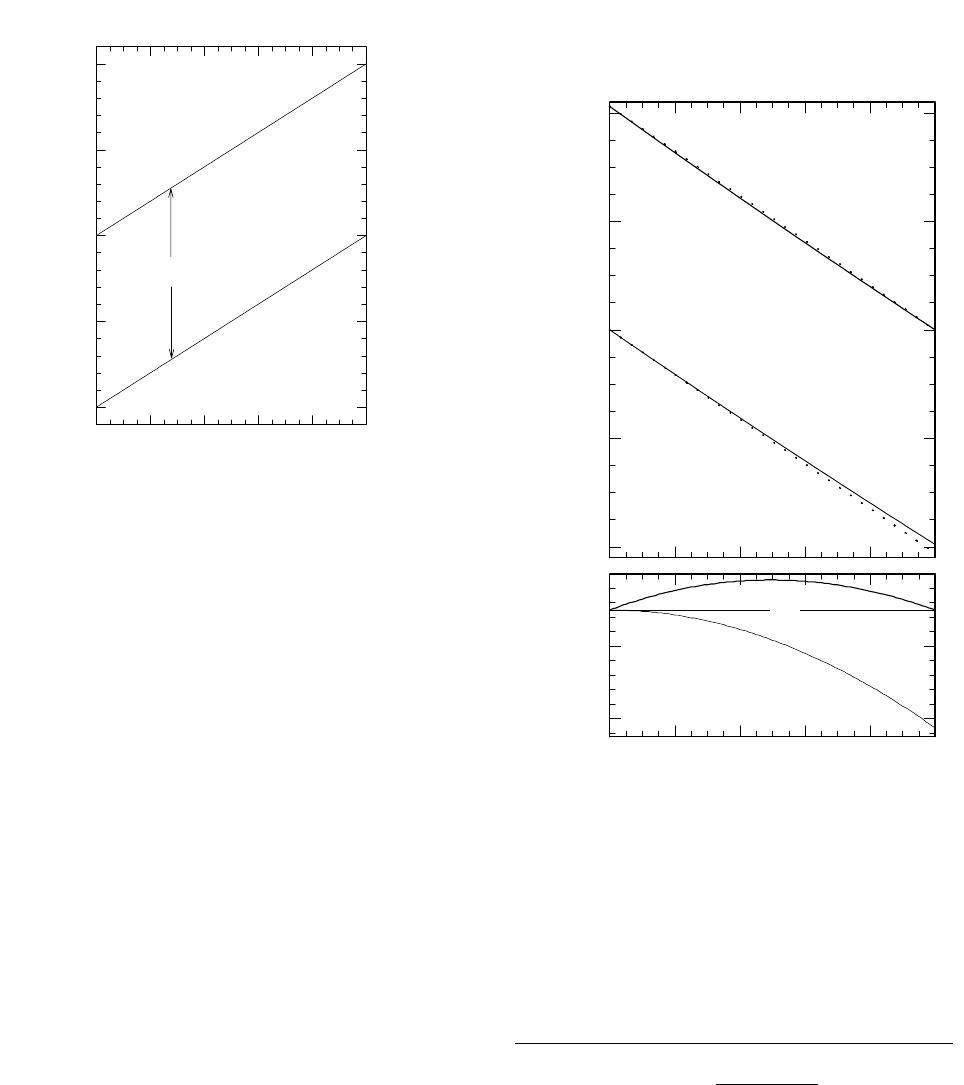
5
between water and gas-phase carbon dioxide at 25°C
(where A is CO
2
and B is H
2
O). The solid and dotted
lines in the larger graph represent the more accurate and
the approximate results, respectively. The lines in the
smaller graph in Figure 4 represent the errors, which
significantly exceed the precision of measurement
(which is typically better than 0.1‰).
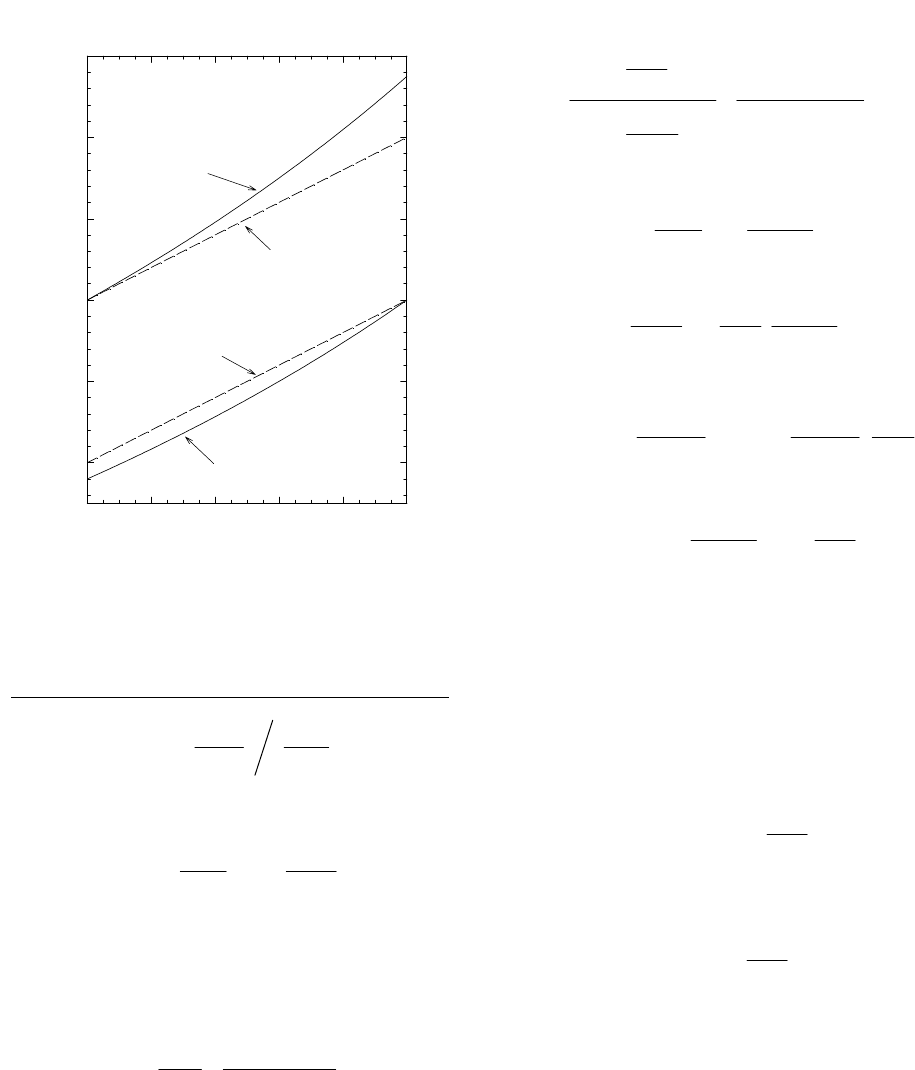
For many hydrogen-isotopic fractionations,
α
differs
from 1.0 by more than 10%. In such cases, the approxi-
mation fails and a magnifying lens is not needed to see
the difference between the accurate and the approximate
results. An example is shown in Figure 5.
Irreversible reaction, closed system. The goal is to
determine the isotopic relationship between the reactants
and products over the course of the reaction, starting
with only reactants and ending with a 100% yield of
products. We’ll consider the general reaction R → P
(Reactants → Products). If the rate is sensitive to
isotopic substitution, we’ll have
α
P/R
≠ 1, where
α
P/R
≡ R
P,i
/R
R
(30)
In this equation,
α
P/R
is the fractionation factor, R
P,i
is
the isotope ratio (e. g.,
13
C/
12
C) of an increment of
product and R
R
is the isotope ratio of the reactant at the
same time. Following the approach of Mariotti et al.
(1981) and expressing R
P,i
in terms of differential quan-
tities, we can write
lRhR
lPhP
P/R
dd
m/m
m/m
=
α
(31)
where the ms represent molar quantities and the sub-
scripts designate the
heavy and light isotopic species of
the
Product and Reactant. In absence of side reactions,
dm
hP
= -dm
hR
and dm
lP
= -dm
lR
. Employing these
substitutions, the equation can be expressed entirely in
terms of quantities of reactant:
f
B
0.00.20.40.60.81.0
δ
Σ
- ε
A/B
δ
A
δ
B
δ
Σ
+ ε
A/B
δ
Σ
ε
A/B
δ
Σ
δ
, ‰
Figure 3. General form of a diagram depicting iso-
topic compositions of species related by a reversible
chemical reaction acting in a closed system.
f
B
0.00.20.40.60.81.0
δ
Σ
+ ε
A/B
δ
A
δ
B
δ
Σ
- ε
A/B
δ
Σ
ε
A/B
δ
Σ
δ
, ‰
Figure 4. Graphs showing results of both accurate
and approximate calculations of isotopic composi-
tions of reactants and products of a reversible reac-
tion in a closed system. The dotted lines in the upper
graph are drawn as indicated in Figure 3 and by equa-
tions 28 and 29. The solid lines are based on equa-
tions 26 and 27. The differences between these treat-
ments are shown in the smaller graph.
f
B
0.00.20.40.60.81.0
δ
, ‰
-40
-20
0
20
40
δ
A
δ
B
α
A/B
= 1.0412
δ
Σ
= 0
δ
B
f
B
0.00.20.40.60.81.0
Error, ‰
-1.5
-0.5
0.5
δ
A
6
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
lR
lR
hR
hR
P/R
dd
m
m
m
m
α
(32)
Separating variables and integrating from initial condi-
tions to any arbitrary point in the reaction, we obtain
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
hR,0
hR
lR,0
lR
P/R
ln ln
m
m
m
m
α
(33)
where the subscript zeroes indicate quantities of
l
R and
h
R at time = 0.
It is convenient to define f as the fraction of reactant
which remains unutilized (i. e., 1 - f is the fractional
yield). Specifically:
lR,0hR,0
lRhR
R,0
R
mm
mm
m
m
f
+
+
==
(34)
Avoiding approximations introduced by Mariotti et al.
(1981), we rearrange this equation to yield exact substi-
tutions for the arguments of the logarithms in equation
33. For example:
f
Rm
Rm
m
m
m
m
m
m
=
+
+
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
)1(
)1(
1
1
R,0lR,0
RlR
lR,0
hR,0
lR,0
lR
hR
lR
(35)
Which yields
R
R,0
lR,0
lR
1
1
R
R
f
m
m
+
+
⋅=
(36)
Similar rearrangements yield
R
R,0
R,0
R
hR,0
hR
1
1
R
R
R
R
f
m
m
+
+
⋅=
(37)
So that equation 33 becomes
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
+
+
⋅=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
⋅
R,0
R
R,0R,0
P/R
1
1
ln
1
1
ln
R
R
R
R
f
R
R
f
RR
α
(38)
Which can be rearranged to yield
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
⋅
R,0
R
R
R,0
P/R
ln
1
1
ln
R
R
R
R
f
ε
(39)
an expression which duplicates exactly equation V.17 in
the rigorous treatment by Bigeleisen and Wolfsburg
(1958). Without approximation, this equation relates the
isotopic composition of the residual reactant (R
R
) to that
of the initial reactant (R
R,0
), to the isotope effect (
α
P/R
),
and to f, the extent of reaction.
If the abundance of the rare isotope is low, the
coefficient for f, (1 + R
R,0
)/(1 + R
R
), is almost exactly 1.
In that case, equation 39 becomes
R,0
R
P/R
ln ln
R
R
f =
ε
(40)
Because quantities with equal logarithms must them-
selves be equal, we can write
R,0
R
P/R
R
R
f =
ε
(41)
Equation 41 is often presented as “The Rayleigh Equa-
tion.” It was developed by Lord Rayleigh (John William
Strutt, 1842-1919) in his treatment of the distillation of
liquid air and was exploited by Sir William Ramsey
(1852-1916) in his isolation first of argon and then of
neon, krypton, and xenon. The ratios in these cases were
not isotopic. The concept of isotopes was introduced by
Frederick Soddy (1877-1956) in 1913, long after Strutt
and Ramsey had been awarded the Nobel Prizes in phys-
ics and chemistry, respectively, in 1904. Instead, the
ratios in Rayleigh’s conception pertained to the abun-
f
B
0.00.20.40.60.81.0
δ
, ‰
-100
0
100
200
300
400
Accurate δ
B
Approximate δ
B
Approximate δ
A
Accurate δ
A
α
A/B
= 0.800
δ
Σ
= +100‰
Figure 5. Graph depicting isotopic compositions
of reactants and products of a reversible reaction in a
closed system with an α value typical of hydrogen
isotope effects.
7
dances of Ar, Ne, Kr, and Xe relative to N
2
and, as the
distillation proceeded, relative to each other.
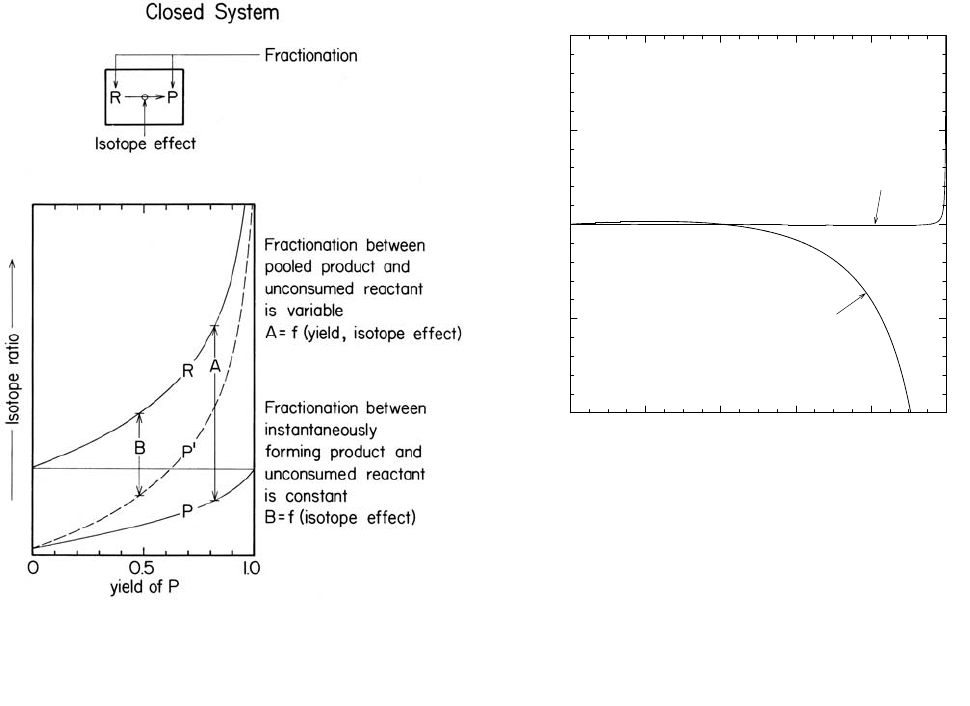
Figure 6 indicates values of R
R
that are in accordance
with equation 41 (viz., the line marked R; on the
horizontal axis, “yield of P” = 1 – f). If the objective is
to use observed values of
δ
P
and/or
δ
R
in order to
evaluate
α
P/R
, a linear form is often desirable. One
which is linear and exact is provided by equation 39.
Values of
δ
must be converted to isotope ratios and the
initial composition of the reactant must be known.
Regression of ln(R
R
/R
R,0
) on ln[f(1 + R
R,0
)/(1 + R
R
)]
will then yield
ε
P/R
as the slope.
By use of approximations, Mariotti et al. (1981)
developed less cumbersome forms. The first is derived
by rewriting equation 40 with the argument of the
logarithm in the delta notation. Rearrangement then
yields
()
(
)
fln1ln1ln
P/RR,0R
ε
δ
δ
++=+ (42)
This is an expression of the form y = a + bx. Regression
of ln(
δ
R
+ 1) on lnf yields a straight line with slope
ε
P/R
.
A second form is very widely applied. Noting that
ln[(1 + u)/(1 + v)] ≅ u – v when u and v are small relative
to 1, Mariotti et al. (1981) simplified eq. 42 to obtain
δ
R
=
δ
R,0
+
ε
P/R
·lnf (43)
This is also an expression of the form y = a + bx. More-
over, it is an equation in which all terms can be expres-
sed in permil units. Regression of
δ
R
on lnf will yield
ε
P/R
as the slope and
δ
R,0
, which need not be known
independently, as the intercept.
The approximations leading to equations 42 and 43
can lead to systematic errors. These are examined in
Figure 7, which is based on values of
δ
and
ε
that are
typical for
13
C. Equation 42 is based on the approxi-
mation that m
lR
/m
lR,0
does not differ significantly from
m
R
/m
R,0
(cf. eq. 34). This is evidently much more
satisfactory than the approximation leading to equation
43, which produces systematic errors that are larger than
analytical uncertainties for values of f < 0.4. Equation 43
should never be used in hydrogen-isotopic calculations,
for which the approximation u ≈ v << 1 is completely
invalid.
Equations 39-43 pertain to values of
δ
R
, the isotopic
composition of the reactant available within the closed
system. Figure 6 also shows lines marked
P and P′ rep-
resenting respectively the isotopic compositions of the
pooled product and of the product forming at any point
in time. The relationship between R and P′ always
follows directly from the fractionation factor:
Figure 6. Schematic representation of isotopic
compositions of reactants and products for an irrever-
sible reaction in a closed system.
f
0.00.20.40.60.81.0
Error in
δ
R
, ‰
-2
-1
0
1
2
Equation 43
Equation 42
ε
P/R
= -30‰ (eq. 43) = -0.030 (eq. 42)
δ
R,0
= -8‰ (eq. 43) = -0.008 (eq. 42)
R
STD
= 0.011180
Figure 7. Errors in values of
δ
R
calculated using
equations 42 and 43.
8
1
1
R
P
R
P
P/R
+
+
==
′′
δ
δ
α
R
R
(44)
As noted in Figure 6, this leads to a constant isotopic
difference (designated
B in the Figure) between R and P′.
Initially, both the pooled product, P, and P′ are depleted
relative to R by the same amount. As the reaction pro-
ceeds, the isotopic composition of P steadily approaches
that of the initial reactant. The functional relationship
can be derived from a mass balance:
m
R,0
δ
R,0
= m
R
δ
R
+ m
P
δ
P
(45)
substituting m
R
/m
R,0
= f and m
P
/m
R,0
= 1 - f, combina-
tion of equations 43 and 45 yields
δ
P
=
δ
R,0
– [f/(1 – f)]
ε
P/R
·lnf (46)
an expression which shows that the regression of
δ
P
on
[f/(1 – f)]·lnf will yield
ε
P/R
as the slope.
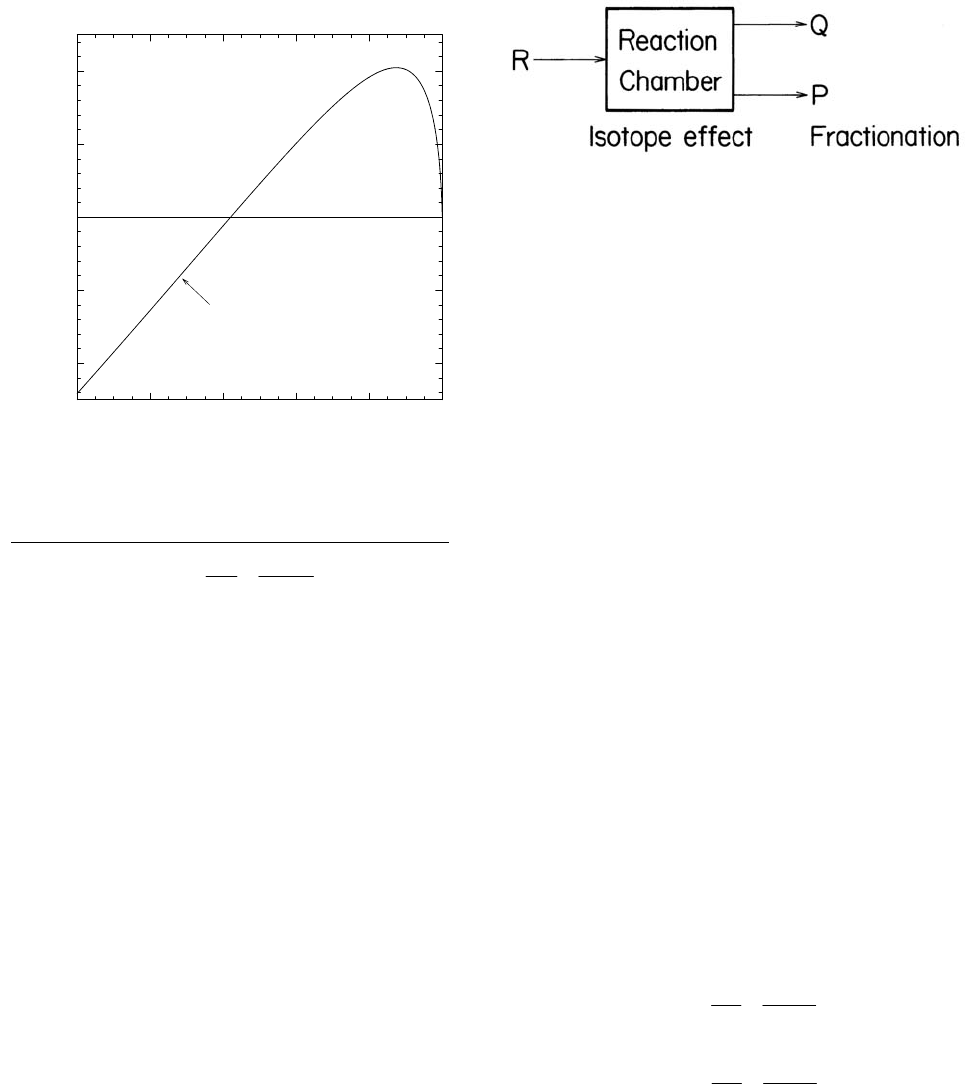
Systematic errors associated with equation 46, sum-
marized graphically in Figure 8, are smaller than those in
equation 43 (note the differing vertical scales in Figs. 7
and 8).
In practical studies of isotope effects, the most vexing
problem is usually not whether to accept approximations
but instead how to combine observations from multiple
experiments. The problem has been explored systemati-
cally and very helpfully by Scott et al. (2004), who have,
in addition, concluded that calculations based on equa-
tion 42 are most likely to provide the smallest uncertain-
ties. Notably, they recommend regression of lnf on ln(
δ
R
+ 1), thus necessitating transformation of the regression
constants in order to obtain a value for
ε
P/R
. Although
both f and
δ
R
are subject to error, use of a Model I linear
regression, and thus assuming that errors in
δ
R
are small
in comparison to those in f, is recommended.
Reversible reaction, open system (product lost).
Atmospheric moisture provides the classical example of
systems of this kind. Water vapor condenses to form a
liquid or solid which precipitates from the system.
Vapor pressure isotope effects lead to fractionation of the
isotopes of both H and O. The process of condensation
is reversible, but the evolution of isotopic compositions
is described by the same equations introduced above to
describe fractionations caused by an irreversible reaction
in a closed system. The heavy isotopes accumulate in
the condensed phases. Consequently, the residual reac-
tant (the moisture vapor remaining in the atmosphere) is
described by increasingly negative values of
δ
R
. The
curves describing the isotopic compositions have the
same shape as those in Figure 6, but bend downward
rather than upward.
Reversible or irreversible reaction, open system at
steady state.
A schematic view of a system of this kind
is shown in Figure 9. A reactant, R, flows steadily into a
stirred reaction chamber. Products P and Q flow from
the chamber. The amount of material in the reaction
chamber is constant and, therefore,
QPR
JJJ +
=
(47)
Where J is the flux of material, moles/unit time.
The relevant fractionation factors are
1
1
P
R
P
R
R/P
+
+
==
δ
δ
α
R
R
(48)
and
1
1
Q
R
Q
R
R/Q
+
+
==
δ
δ
α
R
R
(49)
It doesn’t matter whether these fractionations result from
reversible equilibria or from kinetically limited processes
that operate consistently because residence times within
the reactor are constant. As a result of these processes,
the isotopic difference between P and Q can also be
described by a fractionation factor
f
0.00.20.40.60.81.0
Error in
δ
P
, ‰
-0.2
-0.1
0.0
0.1
0.2
Equation 46
ε
P/R
= -30‰
δ
R,0
= -8‰
Figure 8. Errors in values of
δ
P
calculated using
equation 46.
Figure 9. Schematic view of an open system which
is supplied with reactant R and from which products P
and Q are withdrawn.
9
R/P
R/Q
Q
P
P/Q
α
α
α
==
R
R
(50)
Given these conditions, isotopic fractionations for
any system of this kind are described by equations 26
and 27 (or by eq. 28 and 29 if
α
≈ 1), with P and Q
equivalent to A and B and R equivalent to the material
designated by Σ. The value of f
B
is given by J
Q
/J
R
.
Systems of this kind range widely in size. The
treatment just described is conventional in models of the
global carbon cycle, in which the reaction chamber is the
atmosphere + hydrosphere + biosphere, R is recycling
carbon entering the system in the form of CO
2
, and P and
Q are organic and carbonate carbon being buried in
sediments. The value of
α
R/Q
, the fractionation between
CO
2
and carbonate sediments is accordingly ≈ 0.990.
The value of
α
R/P
, the fractionation between CO
2
and
buried organic material is ≈ 1.015. Combination of these
factors as in equation 50 leads to the fractionation
between organic and carbonate carbon,
α
P/Q
≈ 0.975.
The treatment is also appropriate for isotopic frac-
tionations occurring at an enzymatic reaction site. In this
case, the reaction chamber is the microscopic pool of
reactants available at the active site of the enzyme, R is
the substrate, P is the product, and Q is unutilized sub-
strate (thus
α
R/Q
= 1.000). Fractionations occuring in
networks comprised of multiple systems of this kind
have been described by Hayes (2001).
Irreversible reaction, open system (product
accumulated).
Plants exemplify systems of this kind.
Carbon and hydrogen are assimilated from infinite
supplies of CO
2
and H
2
O and accumulate in the biomass.
The problem is trivial, but a particular detail requires
emphasis. The fixation of C or H can be represented by
R → P (51)
The corresponding isotopic relationship can be described
by a fractionation factor
1
1
P
R
P
P/R
+
+
==
R
R
R
δ
δ
α
(52)
The relationship between
δ
R
and
δ
P
is then described by
P/RRP/R
εδαδ +=
P
(53)
This equation is often simplified to this form:
P/RR
εδδ +=
P
(54)
For example, to estimate the
δ
value of the CO
2
that was
available to the plant, an experimenter will often refer to
“a one-to-one relationship” and subtract
ε
P/R
(typically ≈
-20‰) from the
δ
value of the biomass. For carbon, no
serious error will result. The relationship is nearly “one-
to-one” (slope =
α
P/R
≈ 0.980).
For hydrogen, however, this approach leads to
disaster. Any experimenter dealing with
ε
P/R
≈ -200‰, a
value typical of fractionations affecting deuterium,
should remember that the slope of the corresponding
relationship must differ significantly from 1 and that
equation 53 cannot be replaced by equation 54. This
comparison between fractionations affecting carbon and
those affecting hydrogen is summarized graphically in
Figure 10.
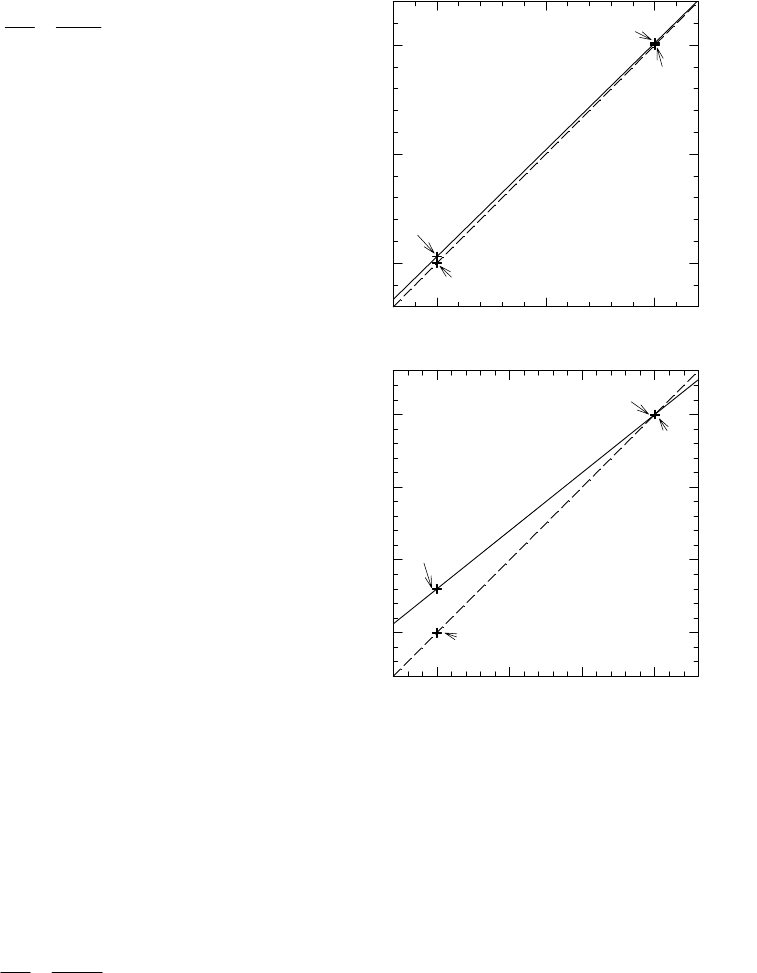
Figure 10. Comparison of fractionations affecting
carbon and hydrogen. In each case, the broken line
represents a “one-to-one” approximation and the
solid line represents the accurate relationship
described by the equation. The approximation is
essentially valid for carbon but seriously in error for
hydrogen.
-15 -10 -5
δ
P
, ‰
-35
-30
-25
-35.0
-34.7
α
P/R
= 0.980
δ
P
= 0.980
δ
P
- 20
-24.9
-25.0
δ
R
, ‰
-300 -200 -100 0
δ
P
, ‰
-500
-400
-300
-200
α
P/R
= 0.800
δ
P
= 0.800
δ
R
- 200
-200
-200
-500
-440
13
C/
12
C
D/H

10
Acknowledgements
Figures 1, 2, 6, and 9 were prepared by Steve
Studley. These notes derive from teaching materials pre-
pared for classes at Indiana University, Bloomington,
and at Harvard University, Cambridge, Massachusetts. I
am grateful to the students in those classes and for
support provided by those institutions and by the
National Science Foundation (
OCE-0228996).
References
Bigeleisen J. and Wolfsberg M. (1958) Theoretical
and experimental aspects of isotope effects in chemical
kinetics. Adv. Chem. Phys.
1, 15-76.
Farquhar, G. D., Ehleringer, J. R., Hubick, K. T.
(1989) Carbon isotope discrimination and photosyn-
thesis. Annu. Rev. Plant Physiol. Plant Mol. Biol.
40,
503-537.
Hayes, J. M. (2001) Fractionation of the isotopes of
carbon and hydrogen in biosynthetic processes. pp. 225-
278 in John W. Valley and David R. Cole (eds.) Stable
Isotope Geochemistry, Reviews in Mineralogy and
Geochemistry Vol. 43. Mineralogical Society of
America, Washington, D. C. pdf available at
http://www.nosams.whoi.edu/general/jmh/index.html
Mariotti A., Germon J. C., Hubert P., Kaiser P., Leto
Ile R., Tardieux A. and Tardieux P. (1981) Experimental
determination of nitrogen kinetic isotope fractionation:
some principles; illustration for the denitrification and
nitrification processes. Pl. Soil
62, 413-430.
McKinney C. R., McCrea J. M., Epstein S., Allen H.
A. and Urey H. C. (1950) Improvements in mass
spectrometers for the measurement of small differences
in isotope abundance ratios. Rev. Sci. Instrum.
21,
724-730.
Mook, W. G. (2000) Environmental Isotopes in the
Hydrological Cycle, Principles and Applications.
Available on line from http://www.iaea.org/program-
mes/ripc/ih/volumes/volumes.htm
Scott, K. M., Lu, X., Cavanaugh, C. M., and Liu, J. S.
(2004) Evaluation of the precision and accuracy of
kinetic isotope effects estimated from different forms of
the Rayleigh distillation equation. Geochim.
Cosmochim. Acta
68, 433-442.
Urey H. C. (1948) Oxygen isotopes in nature and in
the laboratory. Science
108, 489-496.
